1.1 案例背景介绍

我们将模拟一个非常经典的生物学实验——PCR（聚合酶链式反应）体系的优化。我们的目标是找到一个能同时满足高产量、高特异性且错误率低的“黄金配方”。

为了让这个案例更贴近真实世界的研究，我们预设了一个简化的理论模型，其中包含了因子间的交互和非线性关系。这使得找到一个“完美”的解变得极具挑战性，因为各个优化目标之间往往是相互冲突的。

  • 因子 (5个，即我们要调整的变量):

    1. BufferType (缓冲液类型): 分类变量(Categorical), 我们有两种选择: Tris-HCl, HEPES。
    2. MgConcentration (镁离子浓度): 连续变量(Continuous), 范围是 1 到 5 mM。
    3. PrimerConcentration (引物浓度): 连续变量(Continuous), 范围是 100 到 500 nM。
    4. AnnealingTemp (退火温度): 离散变量(Discrete), 水平为: 55, 58, 60, 62°C。
    5. TaqPolymeraseUnits (Taq酶单位): 离散变量(Discrete), 水平为: 0.5, 1.0, 1.5 U。

  • 目标 (3个，即我们希望优化的结果):

    1. Yield (产量): 我们希望最大化 (Maximize)。理论上，它在Mg=3.5, Temp=60°C时达到峰值。
    2. Specificity (特异性): 我们希望最大化 (Maximize)。理论上，它在Primer浓度较低、Temp较高时最好。
    3. Error (错误率): 我们希望最小化 (Minimize)。理论上，它在Taq酶用量和Mg浓度都较低时最小。

理论模型与单项目标最优解 (可用于结果验证)

为了方便您验证AIFactorDesign的优化结果，我们在此公开本次模拟实验背后的数学公式和每个目标的理论最优点。

  • 因子变量定义:

    • B: BufferType (Tris-HCl=1, HEPES=0)
    • M: MgConcentration (1 to 5)
    • P: PrimerConcentration (100 to 500)
    • T: AnnealingTemp (55, 58, 60, 62)
    • E: TaqPolymeraseUnits (0.5, 1.0, 1.5)

  • 目标函数:

    1. Yield (产量): Yield = 80 + 10*B - 2*(M-3.5)^2 - 0.5*(T-60)^2 + 0.1*P/100 + E

      • 理论最优点 (只看Yield):
        • BufferType: Tris-HCl (B=1)
        • MgConcentration: 3.5 mM
        • PrimerConcentration: 500 nM
        • AnnealingTemp: 60 °C
        • TaqPolymeraseUnits: 1.5 U
      • 预期最高产量: 96.5

    2. Specificity (特异性): Specificity = 95 - 0.05*(P-100) + 0.5*(T-55) - (M-1)^2

      • 理论最优点 (只看Specificity):
        • MgConcentration: 1.0 mM
        • PrimerConcentration: 100 nM
        • AnnealingTemp: 62 °C
        • (其他因子无影响)
      • 预期最高特异性: 98.5

    3. Error (错误率): Error = 0.1 + 0.5*(E-0.5)^2 + 0.1*(M-1)

      • 理论最优点 (只看Error):
        • MgConcentration: 1.0 mM
        • TaqPolymeraseUnits: 0.5 U
        • (其他因子无影响)
      • 预期最低错误率: 0.1

理论最优解的冲突:

请注意，最大化产量的最佳Mg浓度（3.5mM）与最大化特异性的最佳Mg浓度（1.0mM）是矛盾的。这正是AIFactorDesign需要解决的核心问题：在这些相互冲突的目标中找到最佳的权衡点。

现在，让我们开始实战操作，看看AIFactorDesign如何在这几个相互冲突的目标之间找到最佳的权衡点！

1.2 快速上手流程 (7个步骤)

步骤1：创建项目

  1. 登录您的AIFactorDesign账户。
  2. 在"My Projects"仪表盘页面，点击右上角的 Create New Project 按钮。
  3. 在弹出的窗口中，输入项目名称 PCR Optimization Demo，然后点击“Save”。

步骤2：因子设计 (Factor Design)

  1. 您会自动进入新项目的“Factor Design”页面。

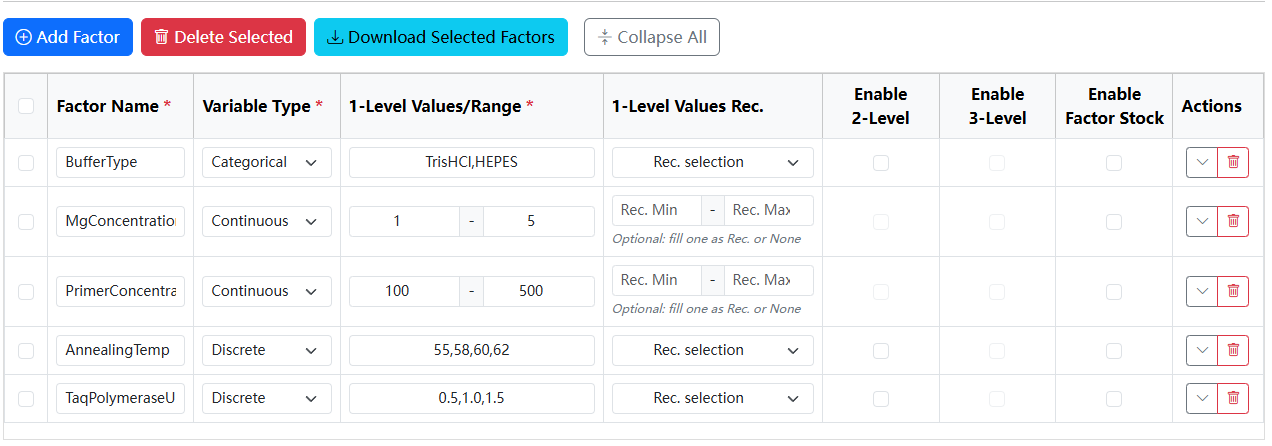
  2. 点击 Add Factor 按钮五次，创建五个因子行。

  3. 按照 1.1 案例背景介绍 中的描述，逐行填写每个因子的Factor Name, Variable Type, 和 1-Level Values/Range。

    • 对于BufferType，类型选Categorical，值输入 Tris-HCl,HEPES。
    • 对于MgConcentration，类型选Continuous，范围输入 1 和 5。
    • ...以此类推，完成所有5个因子的填写。
    • 暂时忽略其他所有列（如Rec., Enable 2-Level等）。
factor_design_demo

步骤3：实验生成 (Experimental Generation)

  1. 滚动到页面底部。
  2. 在 Factor Design Mode 下拉菜单中，选择 Latin Hypercube。
  3. 将 Experiments Runs 设置为 16。
  4. 点击页面右上角的绿色按钮 Experimental Generation。

步骤4：上传训练数据

  1. 点击顶部导航栏中的 Model Learning 模块。
  2. 在“Basic Settings”区域，点击“选择文件”按钮，上传您刚才下载的 pcr_training_data.xlsx 文件。
  3. 在 Target Column Names 输入框中，准确地输入三个目标列的名称，用英文逗号隔开：Yield,Specificity,Error。

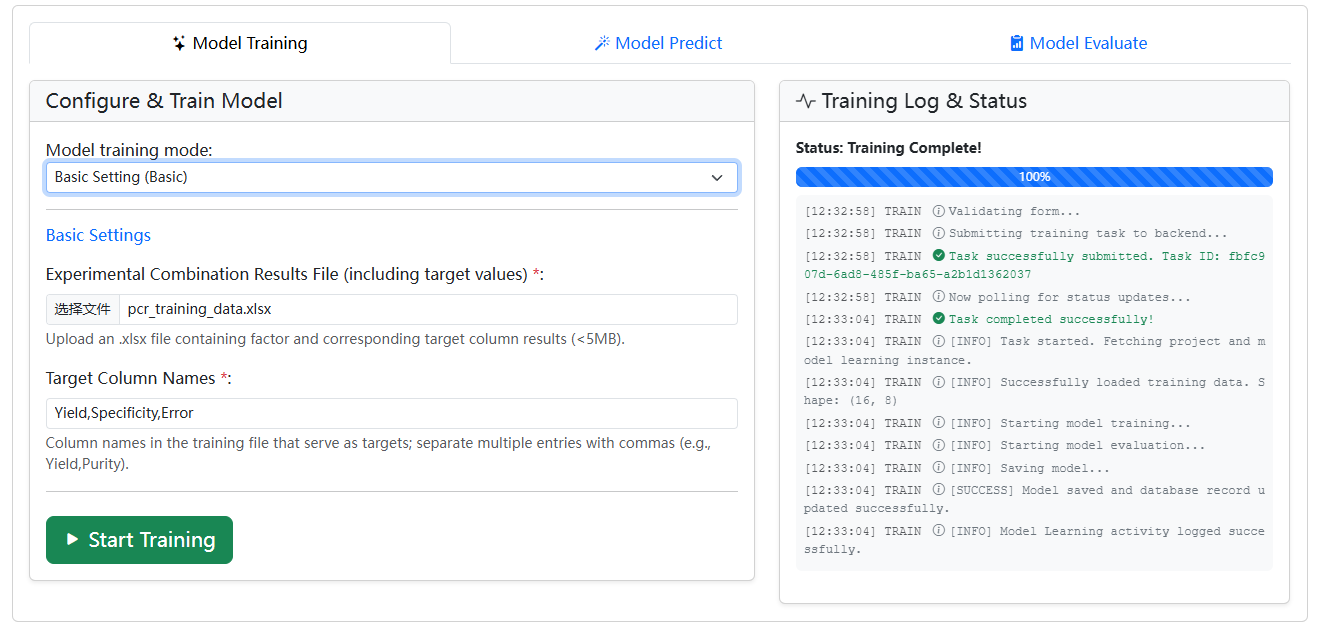
步骤5：模型训练

  1. 保持所有高级参数为默认设置。
  2. 点击绿色的 Start Training 按钮。
  3. 在右侧的“Training Log & Status”区域，您会看到模型开始训练的日志。等待状态变为“Training Complete!”。
model_learning_demo

步骤6：配置优化 (Reagent Optimization)

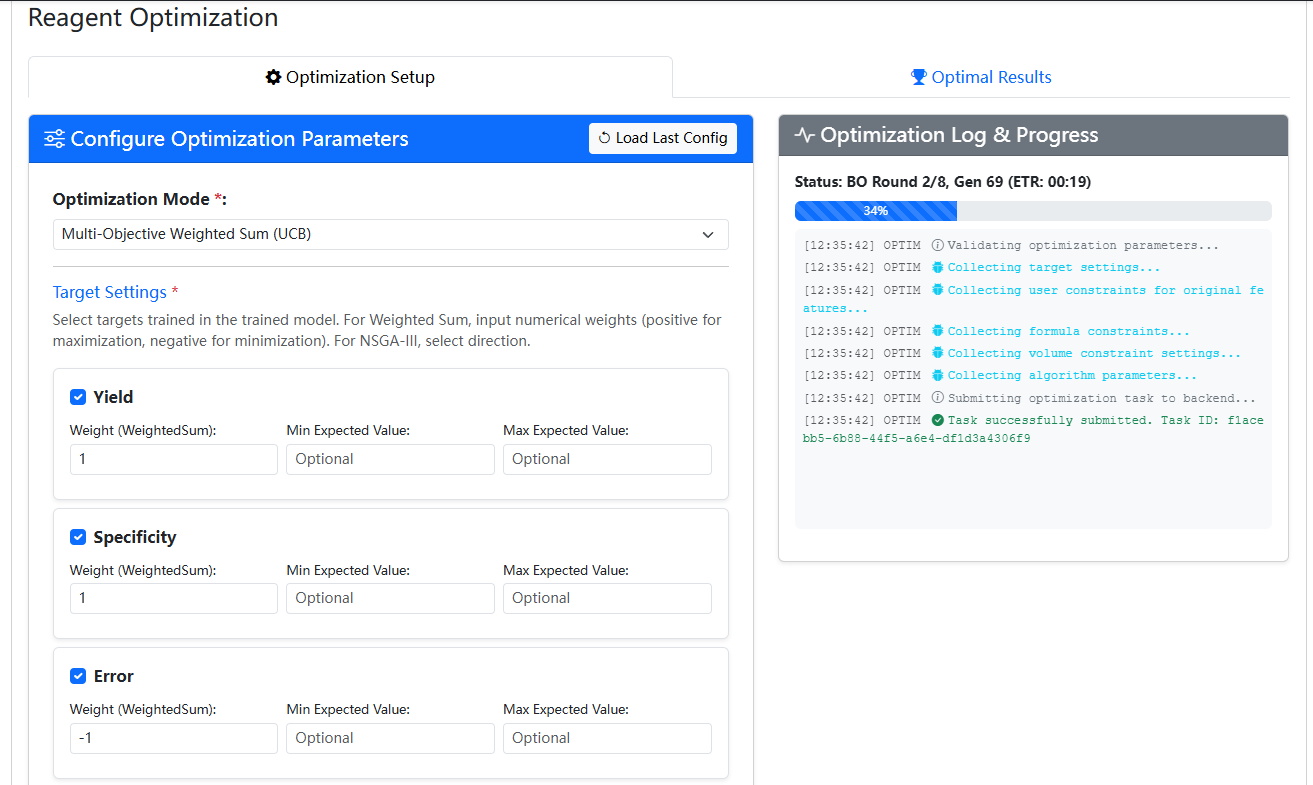
  1. 点击顶部导航栏中的 Reagent Optimization 模块。
  2. 在“Target Settings”区域，您会看到系统已经自动加载了刚刚训练好的三个目标：Yield, Specificity, Error。
  3. 勾选这三个目标前的复选框。
  4. 在展开的输入框中，为每个目标设置权重 (Weight)：
    • Yield: 输入 1 (表示我们想最大化它)
    • Specificity: 输入 1 (表示我们想最大化它)
    • Time: 输入 -1 (表示我们想最小化它，通过设置负权重实现)
reagent_optimization_demo

步骤7：开始优化

  1. 保持所有其他参数为默认设置。
  2. 点击页面底部的 Start Optimization 按钮。
  3. 任务开始后，您可以在右侧的日志区看到优化的实时进度。
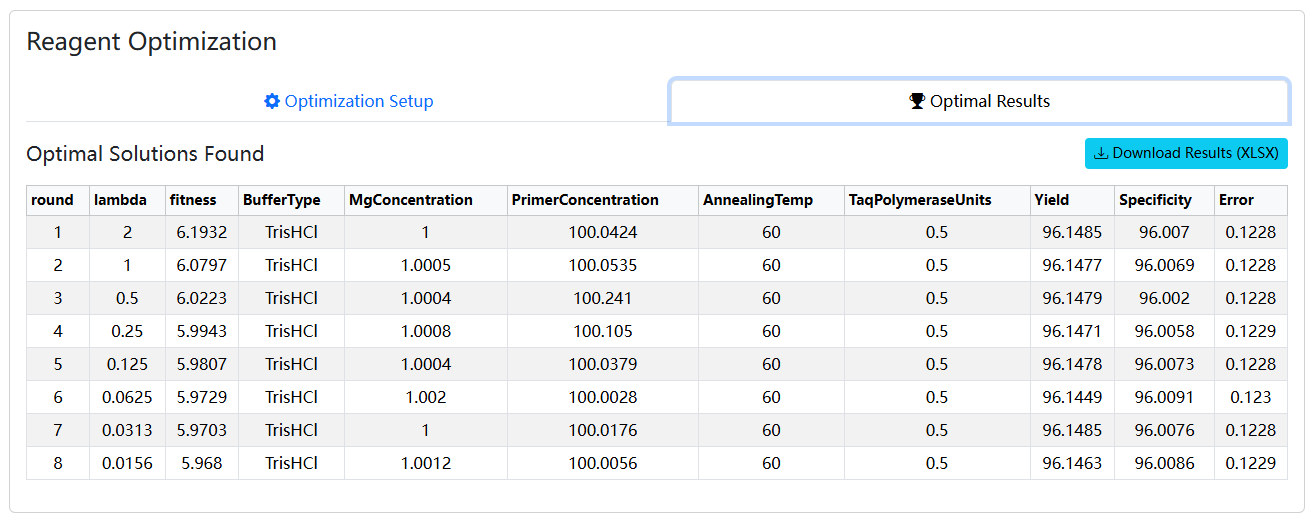
  4. 等待任务完成。完成后，自动切换或手动点击 Optimal Results 标签页。
reagent_optimization_results_demo

1.3 快速上手总结

恭喜您！在 Optimal Results 表格中，您看到的就是AIFactorDesign在综合考虑了产量、特异性和错误率这三个相互冲突的目标后，为您找到的理论上的最佳权衡解（Best Trade-off Solution）。您可以将这个结果与我们理论模型的各个单项最优点进行比较，体会多目标优化的威力。

您已经掌握了AIFactorDesign的核心工作流。接下来的章节，我们将深入探索每个模块的强大功能。