In the vast world of chemistry and materials science, every new discovery can spark a technological revolution. However, the path to these discoveries is often long, expensive, and filled with "trial-and-error" experiments. Scientists are constantly searching for smarter, more efficient research paradigms to find what they're looking for faster and at the lowest possible cost within a sea of possibilities.

In recent years, Bayesian Optimization (BO) has emerged as an experienced AI guide, completely transforming experimental design. By analyzing existing data, it intelligently suggests the next most valuable experiment to run, avoiding blind shots in the dark and significantly accelerating the R&D process.

But scientists are asking: can we go even faster and be more frugal?

The answer is yes, but it comes with a "sweet trap."

The Lure of a "Shortcut": Multi-Fidelity Bayesian Optimization (MFBO)

In many research scenarios, we can not only perform expensive and precise High-Fidelity (HF) experiments (like real-world lab reactions) but also use low-cost computer simulations or preliminary tests to obtain Low-Fidelity (LF) data that is less accurate but still valuable.

This gives rise to Multi-Fidelity Bayesian Optimization (MFBO). Its core idea is incredibly appealing: let cheap "rough estimates" (LF data) guide the expensive "precise measurements" (HF data). It's like sketching a rough map by hand before turning on your power-hungry GPS. In theory, this allows for exploring a much wider experimental space at a fraction of the cost, drastically slashing the overall R&D budget.

However, a critical problem follows: What if the "sketch" is wrong? A poor low-fidelity data source won't just fail to help; it can mislead the entire optimization process, leading to results worse than traditional Single-Fidelity methods (SFBO) and wasting both time and money.

Despite MFBO's immense potential, the academic world has lacked a clear "user manual" to tell researchers: Under what specific conditions should I use MFBO? How can I tell if my low-fidelity data is a valuable asset or a misleading liability?

Clearing the Fog: The First "Best Practices" Guide for MFBO

A joint research team from EPFL (Swiss Federal Institute of Technology Lausanne) and Atinary Technologies Inc. has systematically answered these key questions in a paper published in Nature Computational Science, providing a valuable MFBO Best Practices Guide for chemists and materials scientists worldwide.

A conceptual flowchart of Multi-Fidelity Bayesian Optimization (MFBO), showing how high-fidelity and low-fidelity data are combined to reduce costs.
The core idea of MFBO: combining low-cost rough estimates (LF) with high-cost precise measurements (HF).

Through extensive simulations and real-world chemical scenarios, the research team revealed two core secrets to successfully applying MFBO:

Secret #1: Is the Low-Fidelity Data "Cheap Enough"?

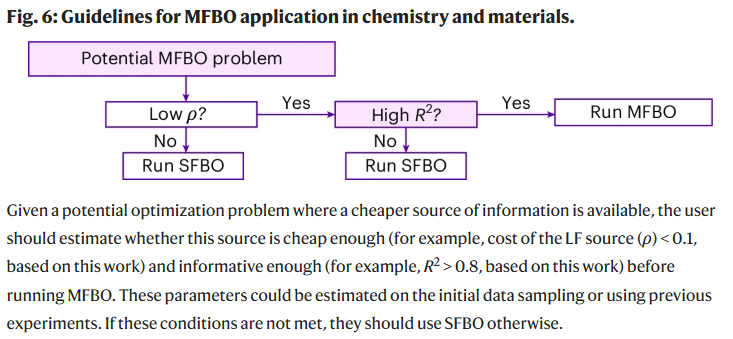
The study found that the cost ratio (ρ) between low-fidelity (LF) and high-fidelity (HF) experiments is a decisive factor. The advantages of MFBO only become apparent when the cost of acquiring LF data is significantly lower than HF.

Practical Guideline: The study recommends that MFBO is ideal when the ρ value is below 0.1, meaning the cost of a low-fidelity experiment is less than 10% of a high-fidelity one. In their experiments, the best performance was observed when ρ was around 0.05.

Secret #2: Is the Low-Fidelity Data "Reliable Enough"?

Being cheap is just the prerequisite; being reliable is key. The researchers used the coefficient of determination (R²) to measure the correlation, or "informativeness," between LF and HF data.

Practical Guideline: Only when the R² value is above 0.8 can the LF data provide dependable guidance for the HF optimization. If the R² is too low, it means the LF data deviates too much from reality, and forcing its use will only lead to negative outcomes.

The MFBO application decision flowchart, asking the two key questions: is it low cost (low p) and highly informative (high R^2)?
The decision flowchart proposed by the researchers, clearly outlining the path to applying MFBO.

Real-World Validation: Slashing Optimization Costs by up to 68%!

To prove the effectiveness of these guidelines, the team rigorously tested MFBO on three real-world chemistry and materials science problems, including:

  1. Optimizing the gas separation performance of Covalent Organic Frameworks (COFs)
  2. Calculating the solvation energy of molecules
  3. Predicting the polarizability of molecules

The results were thrilling! In all scenarios that met the "cheap enough" and "reliable enough" criteria, MFBO far outperformed traditional SFBO. In the COFs benchmark specifically, MFBO successfully reduced the optimization cost required to reach the target performance by 68% (discount Δ = 0.68). This means an experiment that would have originally cost 100 units of budget could now achieve the same result with just 32 units!

Conclusion: Making a Powerful Tool Accessible to Everyone

The most significant contribution of this work is transforming MFBO from a complex tool reliant on expert intuition into a standardized, evidence-based process. It provides a simple yet powerful decision-making framework that allows every materials and molecular researcher to confidently ask before starting an expensive experiment: "MFBO: Should I use it?"

By following this best practices guide, researchers can maximize the advantages of multi-source information, effectively avoid wasting resources, and truly achieve cost reduction and efficiency gains, accelerating the journey to discovering new materials and molecules.

References